| |
| |
|
| |
|
|
КАРТА
САЙТА
ДОПОЛНИТЕЛЬНАЯ
СПРАВОЧНАЯ
И ПОЛНОТЕКСТОВАЯ ИНФОРМАЦИЯ
ИНФОРМАЦИЯ УЧЕБНОГО
НАЗНАЧЕНИЯ:
|
| |
|
| |
|
| |
|
| |
| |
| |
| |
| |
|
| |
|
| |
|
| |
|
| |
| |
| |
|
| |
| |
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
|
| |
НОВЫЕ
ПОСТУПЛЕНИЯ
|
| |
|
| |
НОВЫЕ
ПОСТУПЛЕНИЯ
УЧЕБНЫЙ
ГОД
- 2024
|
| |
НОВЫЕ
ПОСТУПЛЕНИЯ
УЧЕБНЫЙ
ГОД
- 2023
|
| |
|
| |
|
| |
|
|
| СПРАВОЧНАЯ
ИНФОРМАЦИЯ
УЧЕБНОГО НАЗНАЧЕНИЯ
|
|
|
|
| |
| |
Чертеж
и его свойства // Техническое черчение : учебник для учреждений
СПО / А. А. Павлова, Е. И. Корзинова, Н. А. Мартыненко. –
М. : Академия, 2018. – С. 75-80.
Чертежи
появились как средство графического выражения идеи автора (архитектора,
инженера, дизайнера и др.), когда возникла необходимость ее передачи
от одного человека к другому (другим).
Чертеж
– изображение предмета на плоскости, выполненное
по определенным правилам с указанием размеров, масштабов, состава
и других сведений о предмете. Чертеж дает исчерпывающе полную
и однозначную информацию о параметрах формы предмета и его составе.
На чертеже указывают только те сведения, которые необходимы и
достаточны для изготовления изображаемого объекта и его контроля.
Процесс понимания формы изображенного
на чертеже предмета называется чтением
чертежа. Свойство, благодаря которому можно
прочесть чертеж, называется обратимостью
чертежа.
Чертежи всех видов соответствуют
установленным правилам ГОСТ ЕСКД.
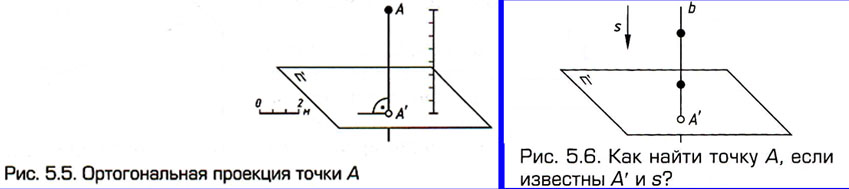
Комплексный
чертеж точки. На рис. 5.5 точка 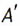 есть
прямоугольная проекция точки А.
Допустим,
что положение точки А нам
неизвестно (рис. 5.6). Сможем ли мы найти его, используя точку есть
прямоугольная проекция точки А.
Допустим,
что положение точки А нам
неизвестно (рис. 5.6). Сможем ли мы найти его, используя точку
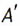 и
зная направление проецирования? Нет, не сможем, так как точка и
зная направление проецирования? Нет, не сможем, так как точка
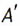 может
быть проекцией любой точки, расположенной на проецирующей прямой
b может
быть проекцией любой точки, расположенной на проецирующей прямой
b
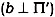 .
Что для этого надо сделать? Ответов может быть несколько: например,
задать расстояние от точки A
до
плоскости проекций (см. рис. 5.5) оно равно 8 м). .
Что для этого надо сделать? Ответов может быть несколько: например,
задать расстояние от точки A
до
плоскости проекций (см. рис. 5.5) оно равно 8 м).
|
|
|
| |
Но
чаще всего для определения положения объекта в пространстве используют
чертежи, построенные способом ортогонального проецирования объекта
на две взаимно-перпендикулярные плоскости проекций.
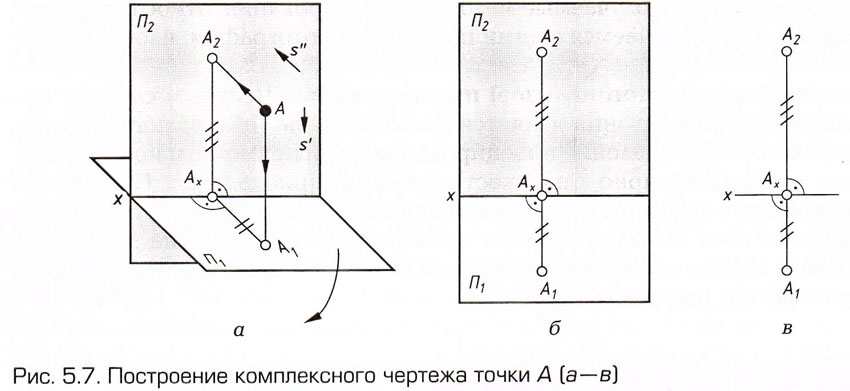
Рассмотрим принцип их построения
на примере простейшего объекта – точки А
(рис.
5.7). Обозначим плоскости проекций 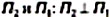 . Линия пересечения плоскостей проекций называется осью
проекций, обозначим ее
х.
. Линия пересечения плоскостей проекций называется осью
проекций, обозначим ее
х.
|
|
Точку
А
ортогонально спроецируем на каждую плоскость проекций по направлениям
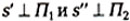 .
Получим две ортогональные проекции точки
A : .
Получим две ортогональные проекции точки
A : 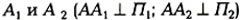 .
. |
Плоскость 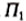 называется горизонтальной плоскостью
проекций,
называется горизонтальной плоскостью
проекций, 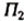 – фронтальной плоскостью проекций.
Точка
– фронтальной плоскостью проекций.
Точка 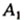 – горизонтальная проекция точки
А;
– горизонтальная проекция точки
А;
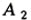 – ее фронтальная проекция.
– ее фронтальная проекция. |
Давайте
повернем горизонтальную плоскость проекций 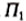 ,
вокруг оси х
на 90° до ее совмещения с фронтальной плоскостью проекций ,
вокруг оси х
на 90° до ее совмещения с фронтальной плоскостью проекций 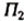 . В результате получим комплексный
чертеж точки
А (или
ее эпюр) (рис. 5.8, б): он состоит из двух
проекций
. В результате получим комплексный
чертеж точки
А (или
ее эпюр) (рис. 5.8, б): он состоит из двух
проекций 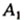 и
и 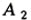 ,
расположенных на одном перпендикуляре ,
расположенных на одном перпендикуляре 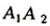 к оси проекций х.
Прямая
к оси проекций х.
Прямая 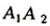 называется линией проекционной
связи. Линия проекционной связи всегда (!)
перпендикулярна соответствующей оси проекций. Такой комплексный
чертеж называется двухкартинным,
так как в его образовании участвуют две плоскости проекций (две
картины).
называется линией проекционной
связи. Линия проекционной связи всегда (!)
перпендикулярна соответствующей оси проекций. Такой комплексный
чертеж называется двухкартинным,
так как в его образовании участвуют две плоскости проекций (две
картины). |
|
| |
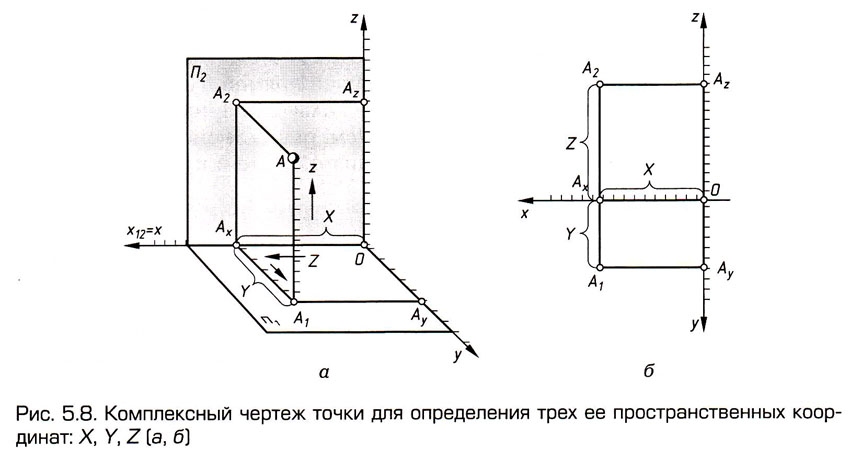
Полученный
таким образом комплекс двух ортогональных проекций мы назвали
чертежом, так как он обладает свойством обратимости. Например
(см. рис. 5.8, а и б), восставив из точки 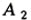 перпендикуляр к
перпендикуляр к 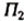 и отложив на нем отрезок
и отложив на нем отрезок 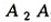 =
= 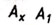 ,
найдем (однозначно) точку
А в
пространстве. ,
найдем (однозначно) точку
А в
пространстве.
Ее положение определяется координатами
X,
Y
и Z
(рис. 5.8, а), измеряемыми в направлении соответствующих координатных
осей х,
у и
z. Оси расположены в соответствующих плоскостях
проекций; в данном примере ось проекций 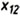 совмещена
с осью координат х.
Комплексный чертеж точки А,
который дает полную информацию о всех ее трех координатах, будет
представлен далее. совмещена
с осью координат х.
Комплексный чертеж точки А,
который дает полную информацию о всех ее трех координатах, будет
представлен далее.
|
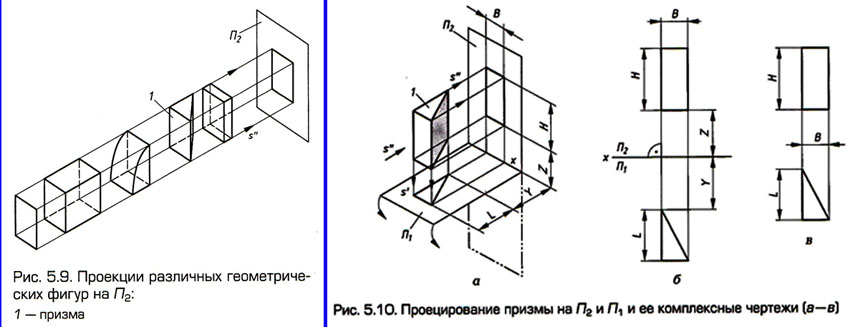
Безосный
комплексный чертеж. Рассмотрим пример проецирования
призмы 1
на
какую-либо одну плоскость проекций, например, на 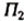 (рис. 5.9). Ясно, что одну ее фронтальную проекцию – прямоугольник
– нельзя назвать чертежом, потому что такой же прямоугольник мы
получим, проецируя различные объемные и плоские формы, как это
показано на рис. 5.9.
(рис. 5.9). Ясно, что одну ее фронтальную проекцию – прямоугольник
– нельзя назвать чертежом, потому что такой же прямоугольник мы
получим, проецируя различные объемные и плоские формы, как это
показано на рис. 5.9. |
Для
получения чертежа призмы поступим аналогично примеру с точкой
А
(см. рис. 5.7). Введем еще одну – горизонтальную – плоскость проекций 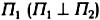 и построим на ней горизонтальную проекцию призмы – прямоугольный
треугольник (рис. 5.10, а). После этого совместим
и построим на ней горизонтальную проекцию призмы – прямоугольный
треугольник (рис. 5.10, а). После этого совместим 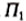 с
с 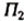 и получим комплексный чертеж призмы (рис. 5.10, б). По такому
чертежу можно определить как параметры формы этой призмы (ее высоту
Н,
ширину
В
и длину L),
так и параметры положения Y
и
Z.
и получим комплексный чертеж призмы (рис. 5.10, б). По такому
чертежу можно определить как параметры формы этой призмы (ее высоту
Н,
ширину
В
и длину L),
так и параметры положения Y
и
Z. |
|
| |
Если
же нас интересуют только параметры формы этой призмы, то на данном
комплексном чертеже мы можем не показывать ось проекций. Такие
чертежи будем называть безосными.
На безосных чертежах также необходимо строго соблюдать проекционную
связь между фронтальной и горизонтальной проекциями объекта (рис.
5.10, в). При этом надо помнить, что линии проекционной связи
всегда перпендикулярны к мысленно проведенной соответствующей
оси проекций. |
Проецирование
на три плоскости проекций. На практике нередки
и такие формы, для отображения которых необходимо ввести профильную
плоскость проекций 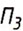 расположенную перпендикулярно
расположенную перпендикулярно 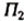 и
и 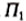 .
Эти три плоскости проекций (три картины) называются
основными. В этом случае появляется еще одна
ось проекций z.
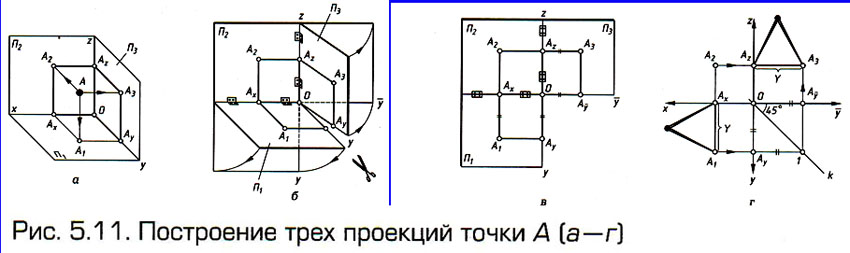
Рис. 5.11, а иллюстрирует
ортогональное проецирование точки
А
на три плоскости проекций. Точки .
Эти три плоскости проекций (три картины) называются
основными. В этом случае появляется еще одна
ось проекций z.
Рис. 5.11, а иллюстрирует
ортогональное проецирование точки
А
на три плоскости проекций. Точки 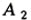 , , 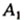 и называются основными
проекциями точки А.
Проекция
и называются основными
проекциями точки А.
Проекция 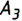 – профильная проекция
точки
А.
– профильная проекция
точки
А. |
|
| |
Для
получения комплексного трехкартинного чертежа точки
А
используются те же приемы, что и для построения ее двухкартинного
чертежа, рассмотренного ранее (см. рис. 5.7). Мысленно разрезав
ось у
(ось у как бы идет на раздвоение) (рис. 5.11, б), поворачиваем
профильную плоскость проекций 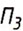 вокруг
оси z
на угол 90° до совмещения ее с фронтальной плоскостью проекций вокруг
оси z
на угол 90° до совмещения ее с фронтальной плоскостью проекций 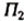 (рис. 5.11, б, в). В результате получаем комплексный трехкартинный
чертеж точки А
(рис. 5.11, г).
(рис. 5.11, б, в). В результате получаем комплексный трехкартинный
чертеж точки А
(рис. 5.11, г). |
На
этом комплексном чертеже появилась новая линия проекционной связи 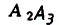 .
Она также перпендикулярна к соответствующей ей оси проекций –
оси z.
Отметив, что координата .
Она также перпендикулярна к соответствующей ей оси проекций –
оси z.
Отметив, что координата 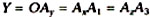 ,
предлагаем самый простой прием графического нахождения на чертеже
профильной проекции точки А.
Этот прием изображен на рис. 5.11, г : построения ведем с
помощью постоянной прямой чертежа k,
она проходит через точку О
и составляет угол 45° с осью
у.
Сколько бы точек ни требовалось отобразить на профильной плоскости
проекций, прямая
k
всегда единственная, ее надо строить только один раз. ,
предлагаем самый простой прием графического нахождения на чертеже
профильной проекции точки А.
Этот прием изображен на рис. 5.11, г : построения ведем с
помощью постоянной прямой чертежа k,
она проходит через точку О
и составляет угол 45° с осью
у.
Сколько бы точек ни требовалось отобразить на профильной плоскости
проекций, прямая
k
всегда единственная, ее надо строить только один раз. |
Кроме
того, для построения профильной проекции 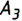 можно также использовать и циркуль-измеритель. При этом величина
его раствора (отрезок
можно также использовать и циркуль-измеритель. При этом величина
его раствора (отрезок 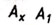 ) должна равняться величине координаты
Y
=
) должна равняться величине координаты
Y
= 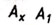 (см. рис. 5.11, г).
(см. рис. 5.11, г). |
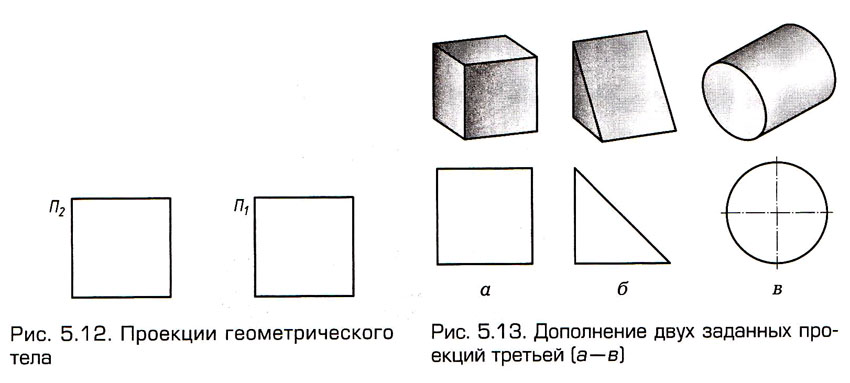
В
качестве иллюстрации необходимости использования в определенных
случаях трехкартинных чертежей приведем такой пример. На рис.
5.12 даны две проекции (два квадрата) некоторого геометрического
тела.
|
|
| |
Какое
именно геометрическое тело они определяют однозначно? В ответ
можно привести сразу несколько вариантов : каждый предмет,
представленный наглядным изображением в верхнем ряду на рис.
5.13, проецируется на 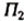 и
и 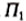 в виде показанных квадратов. Следовательно, для однозначного
понимания формы изображаемого предмета в рассматриваемом случае
две заданные проекции должны быть дополнены третьей, профильной,
проекцией. Например, для цилиндра это круг (см. рис. 5.13, в),
для треугольной призмы – треугольник (см. рис. 5.13, б) и т.д.
в виде показанных квадратов. Следовательно, для однозначного
понимания формы изображаемого предмета в рассматриваемом случае
две заданные проекции должны быть дополнены третьей, профильной,
проекцией. Например, для цилиндра это круг (см. рис. 5.13, в),
для треугольной призмы – треугольник (см. рис. 5.13, б) и т.д.
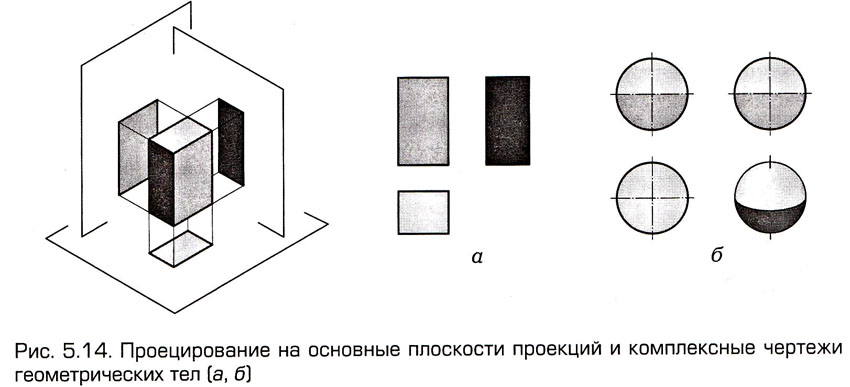
Процесс
проецирования геометрического тела на основные плоскости проекций
иллюстрирует рис. 5.14, а. |
|
| |

Предельная
линейная фигура, за границей которой не проецируется ни одна
точка предмета, называется его очерком
(фронтальным, горизонтальным или профильным), т. е. очерком
предмета можно назвать линейные границы его проекции. Рассмотрим
очерк шара (рис. 5.14, б). Проекциями шара являются три круга,
а его очерками – три окружности, т.е. очерк любого предмета
не имеет заполнения.
Если
фигуру внутри очерка предмета заполнить цветом, например черным,
то получим понятный всем силуэт (рис. 5.15).
Силуэты
лаконичны и выразительны, поэтому такие изображения нередко
используются художниками или фотографами при создании произведений
искусства. Кроме того, строгая графика силуэтов часто встречаются
в рекламе.
|
|
|
|